Dans tous les domaines de la science et de la technologie, les gens doivent choisir leur vocabulaire avec soin. Chaque terme doit avoir le même sens pour tous ses utilisateurs, et exprimer également un concept bien défini qui n'est pas en conflit avec le langage courant. Chaque mesure est influencée par des erreurs qui ne sont pas complètement connues et cela conduit à une incertitude de mesure. Il est important de tenir compte de cette incertitude lors de l'expression de la signification d'une mesure. Nous devons donc décrire précisément l'imprécision de la mesure elle-même. L'article suivant fournit un ensemble de termes importants à bien comprendre et à utiliser correctement par tous les acteurs impliqués dans les mesures.
Comment décrire des mesures correctement
Étalonnage
Une calibration correspond à la comparaison des résultats de mesure obtenus avec une valeur standardisé de référence. Une calibration est réalisée pour valider la qualité des mesures et des ajustements. La valeur de référence standard est fournie, par exemple, par le certificat de masse volumique des liquides standard. Recommandation: 1 à 2 calibrations doivent être réalisées chaque année avec standards certifiés.
Ajustement
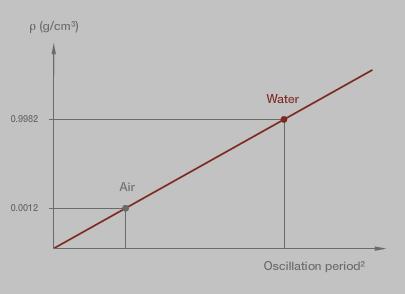
Un ajustement correspond à la modification des constantes de l'instrument pour permettre des mesures correctes et éliminer les erreurs de mesure systématiques. Un ajustement est réalisé après une calibration, sauf si l'écart indiqué est compris dans la plage de tolérance. Pour l'ajustement, le densitomètre utilise les valeurs de masse volumique des standards et les périodes d'oscillation mesurées pour calculer les constantes de l'instrument. Habituellement, deux étalons sont nécessaires pour un ajustement, comme de l'air sec et de l'eau pure (par exemple, bi-distillée), fraîchement dégazée.
Figure 1 : Graphique d'ajustement simplifié d'un densitomètre
Justesse de mesure
La justesse de mesure exprime de manière qualitative dans quelle mesure le résultat de mesure se rapproche de la valeur réelle d’une mesure. Par contraste, la mesure quantitative de l'exactitude est l'imprécision de mesure.
Précision de mesure
La précision de mesure exprime de manière qualitative à quel point les résultats de mesure sont proches les uns des autres dans des conditions de mesure données. La précision peut être exprimée dans des conditions de répétabilité ou de reproductibilité. Il arrive que l’on utilise à tort le terme « précision de mesure » pour désigner la justesse de mesure. Les états de précision et d'exactitude (de gauche à droite) (Figure 2) :
- Pas exact, pas précis
- Exact, pas précis
- Pas exact, précis
- Exact, précis
Figure 2 : États de précision et exactitude
Incertitude de mesure
L’incertitude de mesure définit un intervalle dans lequel la valeur réelle de la mesure est supposée se trouver. L’incertitude de mesure comprend l’incertitude instrumentale (provenant de l’instrument de mesure), l’incertitude liée aux étalons de calibration, ainsi que l’incertitude due au processus de mesure (préparation de l’échantillon, remplissage de la cellule, etc.). L'incertitude de mesure comprend généralement de nombreux composants :
- Certains de ces composants peuvent être évalués à partir de la distribution statistique des résultats ou séries de mesure et peuvent être caractérisés par des déviations standard (évaluation type A conformément au guide ISO/IEC 98-3 :2008).
- Les autres composants, qui peuvent également être caractérisés par des déviations standard, sont évalués à partir des distributions de probabilité présumées basées sur l'expérience ou d'autres informations (évaluation type B conformément au guide ISO/IEC 98-3 :2008).
Incertitude instrumentale de mesure
L’incertitude instrumentale de mesure est la composante de l’incertitude de mesure provenant de l’instrument ou du système de mesure utilisé. L'incertitude de mesure instrumentale est obtenue par l'étalonnage d'un instrument de mesure ou d'un système de mesure.
Répétabilité des mesures
La répétabilité de mesure est la proximité des résultats de mesures successives du même mesurande, effectuées dans les mêmes conditions de mesure. De telles conditions idéales conduisent à une dispersion minimale des résultats de mesure. Les conditions de répétabilité sont :
- Procédure de mesure identique
- Même opérateur
- Même instrument de mesure, utilisé dans les mêmes conditions
- Même emplacement
- Répétition à court terme
La répétabilité peut être exprimée avec l'écart-type de répétabilité. Cet écart-type est calculé à partir de mesures effectuées dans des conditions de répétabilité.
Reproductibilité de mesure
La reproductibilité de mesure est la proximité des résultats de mesures du même mesurande effectuées dans des conditions de mesure modifiées. De telles conditions conduisent à une dispersion maximale des résultats de mesure. Ces conditions de reproductibilité peuvent inclure :
- Principes de mesure
- Méthode de mesure
- Opérateur
- Instrument de mesure
- Standard de référence
- Emplacement
- Conditions d'utilisation
- Heure
Les conditions de mesure modifiées doivent être indiquées. La reproductibilité peut être exprimée avec l'écart-type de reproductibilité. Cet écart-type est calculé à partir de mesures effectuées dans des conditions de reproductibilité définies.
Erreurs de mesure
L'erreur de mesure est une valeur de quantité mesurée moins une valeur de quantité de référence. Les erreurs de mesure aléatoires et les erreurs de mesure systématiques peuvent être distinguées.
figure 3 : Erreurs de mesure
Erreur de mesure aléatoire
L'erreur de mesure aléatoire est le composant d'une erreur de mesure qui varie de manière imprévisible au cours de mesures répétées. Différentes mesures doivent être réalisées pour éliminer les erreurs de mesure aléatoires. La valeur moyenne de ces mesures tend vers la valeur réelle.
Erreur de mesure systématique
L'erreur de mesure systématique correspond à la valeur moyenne qui résulterait d'un nombre infini de mesures de la même grandeur à mesurer effectuées dans des conditions de répétabilité, moins la valeur réelle de la grandeur à mesurer. Les erreurs de mesure systématiques, et leurs causes, sont connues ou inconnues. Une correction peut être appliquée pour compenser une erreur de mesure systématique connue. Erreurs de mesure (de gauche à droite) (Figure 4) :
- Erreur de mesure aléatoire
- Erreur de mesure systématique
Figure 4 : Erreurs de mesures
Biais de mesure
Le biais de mesure est l'estimation d'une erreur de mesure systématique.
Résolution
La résolution est la capacité à résoudre des différences, c'est-à-dire à établir une distinction entre deux choses. Haute résolution signifie être en mesure de résoudre de petites différences. Dans un système numérique, la résolution correspond au plus petit incrément ou à la plus petite étape pouvant être prélevé ou constaté. Dans un système analogique, elle correspond à la plus petite mesure ou différence pouvant être observée en toute certitude. L'erreur la plus commune est la supposition que les instruments ayant une résolution élevée fournissent des résultats plus précis. Haute résolution ne signifie pas nécessairement haute exactitude. L'exactitude d'un système ne peut jamais être supérieure à sa résolution !
Allégorie de la haute résolution :
avec un feutre fin, il est possible de dessiner de petits points.
Allégorie de la faible résolution :
avec un marqueur épais, il n’est pas possible de réaliser des dessins précis.
Figure 5 : Allégorie pour la résolution très fine
Figure 6 : Allégorie pour la résolution grossière
Valeur moyenne arithmétique
La valeur moyenne arithmétique x0 correspond à la somme des valeurs de mesure divisée par le nombre de mesures n :
$$ x _0 = {1 \over n} \sum_{i=1}^n x _i = {{x_1 + x_2 + ... + x_n} \over n} $$
Équation 1 : moyenne valeur arithmétique
x0 … valeur moyenne
xi … nombre de mesures
n... nombres de mesure
La valeur moyenne ne donne aucune information sur la dispersion des résultats de mesure.
Écart-type expérimental (s.d.)
Pour une série de n mesures du même mesurande, l'écart-type expérimental s caractérise la dispersion des résultats. Il est indiqué par la formule :
$$ s = \sqrt{{1 \over n-1} \sum_{i=1}^n (x _i - x_0)^2} $$
Équation 2 : Écart-type expérimental
s ... écart-type empirique
n … nombre de mesures
xi … valeur de mesure de la mesure i
x0 … valeur arithmétique moyenne
La valeur moyenne est souvent citée avec l'écart-type. La valeur moyenne décrit l'emplacement central des données, l'écart-type décrit la diffusion.
