La validation de la température pour la diffraction des rayons X non ambiante (NA-XRD) détermine la relation entre la température du capteur de température dans le dispositif de chauffage et la véritable température à la surface de l'échantillon. Outre d'autres, deux méthodes principales pour la validation de la température sont utilisées dans le NA-XRD :
Cette méthode utilise des substances avec des températures connues de transition de phase cristallographique (solide-solide) ou de points de fusion, et compare les valeurs tabulées de la littérature avec les valeurs mesurées.
Les matériaux de référence pour la validation de la température par transition de phase doivent répondre à certaines exigences pour être adaptés à cette méthode. Ils devraient avoir une température de transition de phase bien établie et fiable, et la transition devrait se produire rapidement pour des résultats précis. Les matériaux avec transition de phase réversible sont préférables, car cela permet de multiples expériences de validation sur le même échantillon. Enfin, le matériau doit être stable et ne doit pas réagir avec les matériaux de fixation ou de support d'échantillon.
La procédure par étapes pour la validation par transformation de phase est donnée ci-dessous :
| Matériau | Température de transition vitreuse | solide-solide / point de fusion | Littérature : |
| KNO₃ | 128.7 | ss | [2] |
| KCIO₄ | 299.4 | s.s. | [2] |
| Ag₂SO₄ | 430 | s.s. | [2] |
| SiO₂ | 573 | s.s. | [3] |
| K₂SO₄ | 583 | s.s. | [3] |
| NaCl | 804 | M.p. | [4] |
| Cu | 1083 | m.p. | [4] |
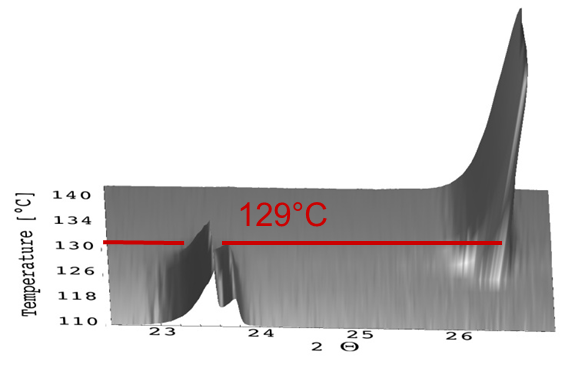
Dans le graphique ci-dessous (Figure 1), les résultats pour KNO3, mesurés dans un accessoire de chauffage pour DRX, sont montrés.
La température de transition de phase mesurée de la structure orthorhombique à la structure trigonal de KNO3 était de 129 °C. Selon la littérature, la température de transition de phase pour cette transition de phase est de 130 °C. Cela signifie que l'écart entre la température affichée et la température réelle n'est que de 1 °C.
Figure 1 : Scans empilés de la transition de phase de KNO₃
Figure 2 : Courbe de validation de la température avec plusieurs transitions de phase / points de fusion
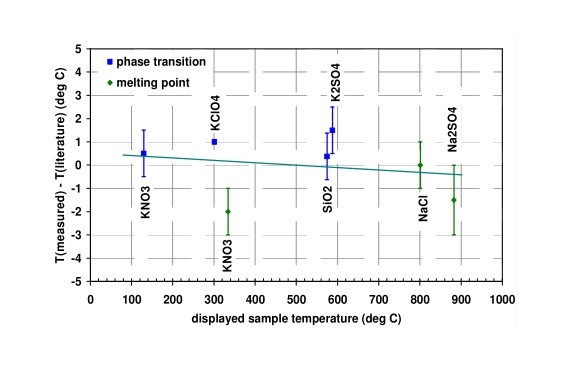
Un inconvénient de la validation par l'utilisation des transitions de phase est qu'une seule substance n'a qu'un nombre limité de transitions de phase. Afin d'avoir une image plus complète du comportement thermique de l'accessoire de chauffage, plusieurs substances doivent être mesurées. (En fonction de la plage de température, cela peut prendre beaucoup de temps.)
Un exemple d'une validation aussi étendue est montré dans la Figure 2.
Cette méthode peut être appliquée si un matériau dont le comportement d'expansion thermique est précisément connu est disponible. La courbe d'expansion thermique d'un certain matériau relie l'augmentation de la taille d'un paramètre de réseau à la température appliquée. Il peut être calculé en utilisant la formule suivante :
\[ \frac{\Delta L}{L_0} = a_0 + a_1 T + a_2 T^2 + a_3 T^3 \]
∆L=L(T)- L0
L(T) … longueur de l'axe du réseau à la température T
L0 … longueur de l'axe du réseau à 293 K
T … température en K
Coefficients d'expansion thermique
La courbe d'expansion thermique pour l'axe c du corindon ressemble, par exemple, à ce qui suit :
\[ \frac{\Delta L}{L_0} = -0.192 + 5.927 \times 10^{-4} T + 2.142 \times 10^{-7} T^2 - 2.207 \times 10^{-11} T^3 \]
∆L=L(T)- L0
L(T) … longueur de l'axe du réseau à la température T
L0 … longueur de l'axe du réseau à 293 K
T … température en K
Inversement, la détermination du paramètre de réseau permet le calcul de la température. Comme les dimensions de l'axe sont disponibles à partir du raffinement de Rietveld, la véritable température à la surface de l'échantillon peut être déterminée.
Les matériaux de référence pour la validation de la température par expansion thermique ont des exigences spéciales. Surtout, les coefficients de dilatation thermique du matériau doivent être bien connus. Pour faciliter l'analyse et réduire les erreurs statistiques, il est également utile d'utiliser des matériaux qui présentent une forte expansion thermique. Le matériau doit également afficher des paramètres de réseau stables sans transitions de phase ni réactions chimiques se produisant pendant le processus de chauffage.
La procédure par étapes pour la validation par transformation de phase est donnée ci-dessous :
Les résultats de ce type de validation de température seront présentés dans le chapitre 1.3.
L'influence des différentes atmosphères gazeuses sur la précision de la température est discutée pour un radiateur à bande. Les conditions suivantes ont été évaluées : Il (pression atmosphérique), N2 (pression atmosphérique) et vide. Il est prévu que l'écart de température entre la température mesurée du capteur de température (soudé par points au bas de la bande chauffante) et la température à la surface de l'échantillon soit le plus élevé sous vide. La raison est que la convection, qui aiderait à transférer la chaleur de la bande à l'échantillon, est complètement absente. Comme la conductivité thermique de He (5,193 KJ/kgK) est beaucoup plus élevée par rapport à N2 (1,040 KJ/kgK), He devrait donner les meilleurs résultats.
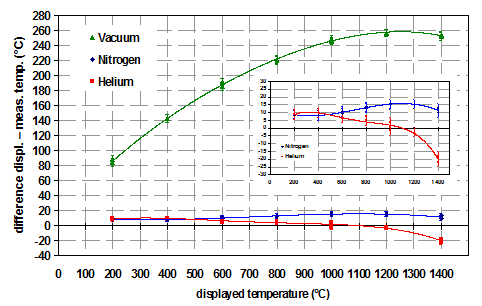
Dans la figure suivante (Figure 3), l'effet de différentes atmosphères gazeuses sur la précision de la température est montré pour une mesure de l'expansion thermique de MgO.
Figure 3 : Résultats de validation pour un chauffage direct en fonction de l'atmosphère gazeuse
Figure 4 : Résultats de validation pour un chauffage direct en fonction de l'atmosphère gazeuse
Il est facilement visible dans la Figure 3 que les hypothèses ci-dessus sont confirmées.
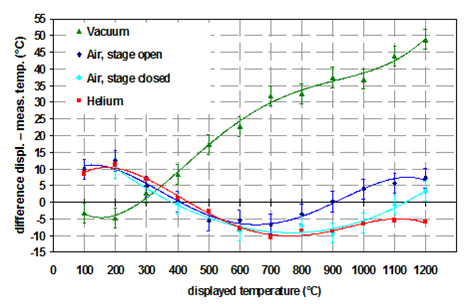
On peut observer les mêmes tendances pour les chauffages d'appoint, mais dans ce cas, les écarts absolus sont beaucoup plus petits en raison de la meilleure homogénéité de température dans les chauffages d'appoint. Dans ce cas, l'expansion thermique de l'axe c de Al2O3 a été utilisée pour la validation (Figure 4).
Figure 5 : Influence de l'épaisseur de l'échantillon sur la précision de la température dans un chauffage direct
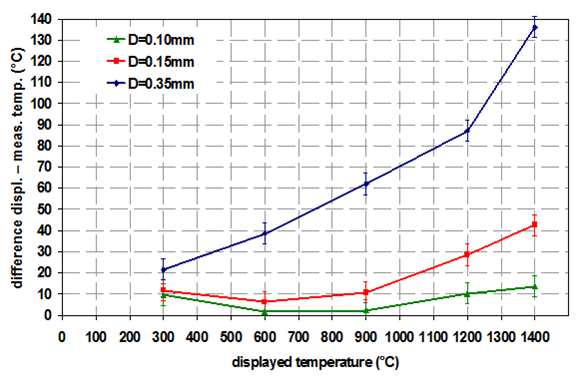
Un grand avantage des chauffages environnementaux est que les propriétés thermiques de l'échantillon ne sont pas si importantes pour la déviation de température. C'est particulièrement vrai pour l'épaisseur de l'échantillon. Pour les chauffages directs, l'épaisseur de l'échantillon a un grand impact sur la déviation de température comme on peut le voir sur la Figure 5. Dans cet exemple, l'expansion thermique de Al2O3 a été mesurée avec un chauffage à bande (=chauffage direct) sous atmosphère d'hélium.
Il est clairement visible que l'épaisseur de l'échantillon a une influence significative sur la déviation de température. Par conséquent, pour les chauffages directs, la meilleure méthode de préparation des échantillons est la suivante : l'échantillon doit être appliqué aussi finement que possible, tout en couvrant complètement la bande de chauffage. Sinon, des signaux supplémentaires de la bande chauffante sont visibles dans le diffractogramme et rendent l'interprétation des données plus difficile.
