De nombreuses substances liquides, gélatineuses ou semi-solides du quotidien sont généralement caractérisées par la mesure de la viscositéd'un échantillon, de sa courbe d'écoulement et de son point de rendement à l'aide de viscosimètres/rhéomètres rotatifs. L'eau est un échantillon typique avec une faible viscosité et n'a pas de point de rendement. Le dentifrice, en revanche, a une viscosité plus élevée et un point de rendement. Le point de rendement nous indique combien de force doit être appliquée pour que le matériau commence à s'écouler. Cet article décrit comment une courbe d'écoulement est mesurée avec un viscosimètre rotatif et comment le point de rendement peut être calculé.
Détermination de la courbe et du seuil d’écoulement avec une viscosimétrie rotative
Mesure avec un viscosimètre/rhéomètre rotatif
Figure 1 : Viscosimètre rotatif : Le moteur de l'instrument fait tourner la masse de mesure à l'intérieur d'une tasse remplie d'échantillon.
La plupart des viscomètres/rhéomètres rotatifs fonctionnent selon le principe de Searle : Un moteur entraîne un bob à l'intérieur d'une tasse fixe. La vitesse de rotation du pendule est préréglée et produit un certain couple moteur nécessaire pour faire tourner le pendule de mesure. Ce couple doit surmonter les forces visqueuses de la substance testée et est donc une mesure de sa viscosité. Un viscosimètre rotatif mesure la viscosité dynamique [ƞ] d'un échantillon. La loi de Newton définit la viscosité dynamique η comme la contrainte de cisaillement divisée par le taux de cisaillement[3]. Lorsque nous mesurons la viscosité sur un viscosimètre rotatif, nous appliquons à l'échantillon une certaine contrainte de cisaillement ou un certain taux de cisaillement, respectivement. $\eta = {{\tau} \over {\dot{\gamma}}}$
Equation 1: LA loi de viscosité de Newton
$\eta$ ... Viscosité dynamique [Pa.s]
$\tau$ ... Contrainte de cisaillement [Pa]
${\dot{\gamma}}$ ... Taux de cisaillement [s-1]
couple × facteur de conversion = contrainte de cisaillement Dans un test de rotation typique, le taux de cisaillement est préréglé. Cela signifie que le viscosimètre traduit le taux de cisaillement choisi en vitesse et mesure le couple résultant, qu'il traduit ensuite en contrainte de cisaillement[3]. Une telle mesure, où le taux de cisaillement est augmenté et la contrainte de cisaillement résultante est mesurée, est appelée une courbe d'écoulement.
Courbe d'écoulement
Définition d'une courbe de flux
Les tests de rotation typiques sont des fonctions de viscosité qui dépendent du taux de cisaillement, de la contrainte de cisaillement, du temps ou de la température. Les résultats d'un test de rotation peuvent être affichés d'une part sous forme de diagramme de courbe de flux montrant les valeurs de contrainte de cisaillement résultantes, et d'autre part sous forme de la fonction de viscosité correspondante. Une mesure sur un viscosimètre/rhéomètre rotatif dans laquelle le taux de cisaillement est augmenté par étapes et la contrainte de cisaillement respective est déterminée pour chaque taux de cisaillement est appelée une courbe d'écoulement. Un matériau peut montrer différents comportements d'écoulement tels que le comportement idéalement visqueux, le comportement pseudoplastique et le comportement dilatant. Dans presque toutes les étapes de production, la viscosité des échantillons alimentaires a un grand impact, par exemple dans le processus de mélange des substances laitières et pour la génération de nouvelles formulations pour les sauces végétales. À faibles taux de cisaillement, la viscosité de l'échantillon au repos est mesurée (par exemple, lorsqu'il est stocké dans la bouteille) et à des taux de cisaillement élevés, la viscosité de l'échantillon en mouvement (par exemple, lors de l'ingestion ou du secouage de l'échantillon) est testée. La crème de noisette, par exemple, devrait avoir une viscosité définie lorsqu'elle est étalée sur une tranche de pain et ne devrait pas être trop liquide ni trop épaisse.
Mesure de courbe d'écoulement
Figure 2 : Réglages du viscosimètre/rhéomètre pour une courbe d'écoulement
Une courbe d'écoulement peut être générée via des paramètres prédéfinis sur le viscosimètre/rhéomètre rotatif :
- Le taux de cisaillement est augmenté par étapes avec une durée de point de mesure définie pour chaque point.
- La température et d'autres conditions ambiantes sont constantes.
La courbe de flux résultante montre la contrainte de cisaillement par rapport à la vitesse de cisaillement. En général, les points de mesure individuels sont reliés par des lignes pour montrer la courbe d'écoulement.
Courbe d'écoulement des substances idéalement visqueuses
Pour des échantillons idéalement visqueux ou dits newtoniens, la contrainte de cisaillement augmente linéairement avec l'augmentation de la vitesse de cisaillement. La figure 4 montre une telle courbe d'écoulement de deux échantillons newtoniens, l'échantillon (a) étant plus visqueux que l'échantillon (b). La viscosité des échantillons ne change pas avec l'augmentation du taux de cisaillement. Des exemples typiques seraient l'huile d'olive pour l'échantillon (a) et l'eau pour l'échantillon (b).
Figure 3 : Courbes d'écoulement de deux fluides visqueux idéaux différents
Courbe d'écoulement des substances à écoulement cisaillant
Pour les matériaux ayant un comportement d'écoulement à fluage, le gradient de la contrainte de cisaillement diminue à des taux de cisaillement plus élevés. Cela signifie que la viscosité de l'échantillon est devenue plus faible à des taux de cisaillement plus élevés. C'est un comportement typique de nombreux matériaux de la vie quotidienne, par exemple des cosmétiques tels que des crèmes et des lotions, des échantillons alimentaires tels que du ketchup ou du chocolat fondu, ainsi que des échantillons chimiques tels que des peintures et des revêtements. Voir la figure 4.
Figure 4 : Courbes d'écoulement d'un fluide d'amincissement par cisaillement
Figure 5 : Courbes d'écoulement d'un fluide d'amincissement par cisaillement
Courbe d'écoulement des substances à écoulement cisaillant
Pour les matériaux ayant un comportement d'écoulement à fluage, le gradient de la contrainte de cisaillement diminue à des taux de cisaillement plus élevés. Cela signifie que la viscosité diminue à des gradients de cisaillement plus élevés, p. ex. lors de la déglutition. C'est un comportement d'écoulement relativement rare, généralement observé dans des échantillons avec une forte teneur en solides tels que des suspensions céramiques, des dispersions d'amidon ou des composites dentaires.
Calcul du point de rendement de Bingham
Définition du point de rendement
Le point de rendement est la valeur de contrainte de cisaillement la plus basse au-dessus de laquelle un matériau se comportera comme un fluide, et en dessous de laquelle le matériau agira comme une matière solide[2] Des exemples typiques de matériaux ayant un point de rendement sont les crèmes, le ketchup, le dentifrice et les scellants. Le point d'écoulement est la force minimale qui doit être appliquée à un échantillon pour qu'il commence à s'écouler. Les substances avec une contrainte de rendement ne commencent à s'écouler que lorsque la force extérieure agissant sur elles est supérieure à leurs forces structurelles internes. En dessous du point de rendement, la substance montre un comportement « semblable à un solide ». Par exemple, le dentifrice ne sort pas de son tube si aucune force externe n'est appliquée. En dessous du point de rendement, il se comporte comme un solide. Le point de rendement peut être dépassé en augmentant les forces de cisaillement (par exemple, en appuyant sur le tube). Au-dessus du point de rendement, l'échantillon s'écoule (hors du tube) et se comporte comme un liquide. Le point de rendement est d'une importance vitale pour de nombreuses questions et applications pratiques, par exemple pour le contrôle de la qualité des produits finis ou pour l'optimisation du processus de production.
Figure 6 : Le point de rendement est la force minimale qui doit être appliquée à un échantillon pour qu'il commence à s'écouler.
Calcul du point de rendement avec une courbe de flux
Le point de rendement n'est pas une constante matérielle mais dépend de la méthode de mesure et d'analyse utilisée. Il existe de nombreuses méthodes différentes disponibles. Sur les viscosimètres rotatifs, la limite d'élasticité est souvent calculé à partir des courbes d'écoulement mesurées avec une augmentation linéaire de la vitesse en utilisant des modèles de régression mathématique. Le point de rendement n'est pas mesuré directement, mais calculé à l'aide de fonctions modèles (par exemple, Bingham, Casson ou Herschel-Bulkley). Pour tous ces modèles d'approximation, la valeur du point de rendement ${ au}_0$ (prononcé "tau zéro") est déterminée par extrapolation de la courbe d'écoulement vers une valeur de faible taux de cisaillement. Chaque modèle fonctionnel différent produit généralement un point de rendement différent car le calcul est différent.
Figure 7 : Courbe d'écoulement de deux matériaux à écoulement pseudoplastique différents
Figure 8 : Modèle de Bingham pour le calcul du point d'écoulement
Calcul du point de rendement de Bingham
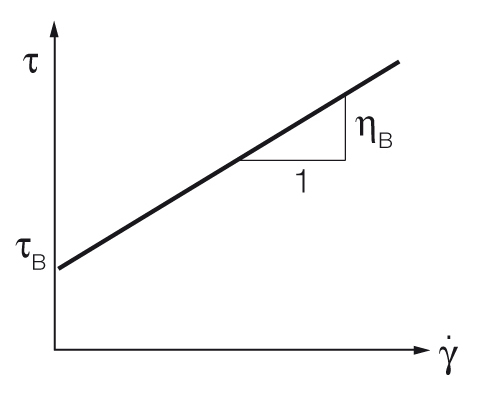
La régression de Bingham calcule le point de rendement avec une pente constante[4, 5]. Il est principalement utilisé lorsque le matériau présente une pente constante au-dessus de la contrainte d'écoulement, par exemple certains types d'aliments ou de cosmétiques. Historiquement, avant l'utilisation des ordinateurs, c'était un moyen très facile de déterminer le point de rendement. Voir la figure 8.
$$\tau = \tau_B + \eta_B \cdot {\dot{\gamma}}$$
Équation 2 : équation de Bingham pour le point d'écoulement
$\tau$ ... contrainte de cisaillement [Pa]
$\tau_B$ ... Bingham point d'écoulement [Pa]
$\eta_B$ ... Bingham viscosité [Pa.s]
${\dot{\gamma}}$ ... taux de cisaillement [s-1]
Calcul du point de rendement de Bingham
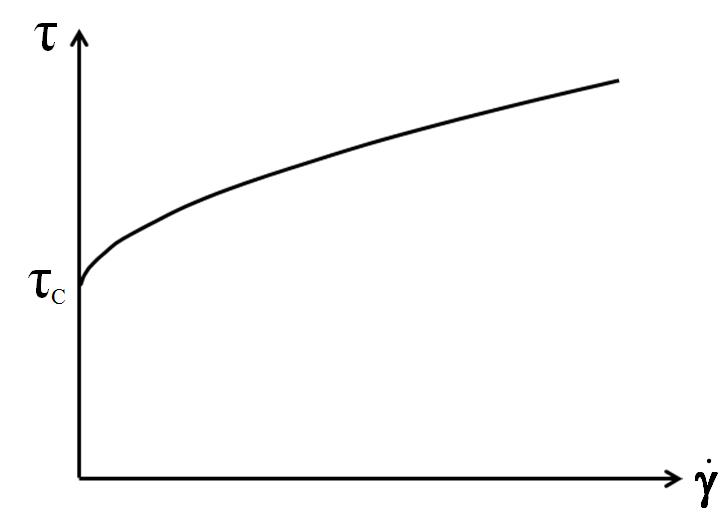
Pour le calcul du point de rendement de Casson, un ajustement de courbe est effectué en utilisant une fonction racine carrée[6]. Cela prend en compte la courbure de la courbe et est donc souvent mieux adapté aux matériaux à écoulement de cisaillement et à épaississement de cisaillement que le calcul de Bingham. Il est généralement utilisé pour des produits alimentaires tels que le chocolat. Voir la figure 9.
$$\sqrt{\tau} = \sqrt{\tau_c} + \sqrt{\eta_c \cdot \dot\gamma}$$
Équation 3 : équation de Bingham pour le point d'écoulement
$\tau$ ... contrainte de cisaillement [Pa]
$\tau_B$ ... Casson point d'écoulement [Pa]
$\eta_c$ ... Bingham viscosité [Pa.s]
${\dot{\gamma}}$ ... taux de cisaillement [s-1]
Calcul du point de rendement Herschel-Bulkley
La régression de Herschel-Bulkley décrit la courbe d'écoulement d'un matériau avec une contrainte d'écoulement et un comportement de fluage à cisaillement ou d'épaississement à cisaillement à des contraintes supérieures à la contrainte d'écoulement[7].
$$\tau = \tau_{HB}+ {c} \cdot \dot\gamma^{p}$$
Équation 4 : équation de Herschel-Bulkley pour le point d'écoulement
$\tau$ ... contrainte de cisaillement [Pa]
$\tau_B$ ... Point de rendement de Herschel Bulkley [Pa]
c ... coefficient d'écoulement, également appelé viscosité de Herschel Bulkley [Pa.s]
${\dot\gamma}$ ... taux de cisaillement [s-1]
p ... exposant, également appelé indice de Herschel Bulkley
$\tau_{HB}$ décrit le point de rendement du matériau. c est le soi-disant "coefficient d'écoulement" ou "indice de consistance" qui décrit la viscosité à un certain taux de cisaillement. Le paramètre p (également appelé "indice de Herschel-Bulkley") décrit le comportement d'écoulement du matériau :
- p < 1 : cisaillement-diluant
- p < 1 : cisaillement-diluant
- p = 1 : Comportement d'écoulement de Bingham
En utilisant ces paramètres d'évaluation, dans la plupart des cas, un meilleur ajustement de courbe sera obtenu qu'avec le modèle de Bingham.
Figure 9 : Modèle de Casson pour le point de rendement
Figure 10 : Modèle de Herschel-Bulkley pour le point d'écoulement
Calcul du point de rendement statique avec la technique de la pale
La détermination du point de rendement statique à l'aide de la technique de la pale est une méthode très rapide, facile et directe pour analyser le point de rendement avec un viscosimètre rotatif d'entrée de gamme. Cette méthode évite les effets de glissement et minimise les changements structurels de l'échantillon lors de l'immersion de la broche. Pour la mesure du point de rendement, un axe à palettes avec quatre à huit lames fines disposées à des angles égaux est utilisé. En insérant l'arbre de l'ailette dans un échantillon pâteux par exemple, la structure de l'échantillon est perturbée seulement légèrement par rapport aux systèmes à cylindres concentriques. Il est important que le diamètre du bécher soit au moins deux fois la taille du diamètre de l'aile. Un changement dans la structure de l'échantillon peut être encore minimisé en utilisant le conteneur d'échantillon original plutôt qu'en versant l'échantillon dans un bécher. La valeur de rendement dépend fortement de la préparation de l'échantillon et du prétraitement de l'échantillon avant de commencer la mesure[8, 9]. Pour mesurer le point de rendement, une vitesse constante et faible est préréglée sur le viscosimètre rotatif. La contrainte de rendement maximale, qui peut être détectée lors de la mesure, est la valeur du point de rendement. Pour illustrer le point de rendement dans un graphique, le couple est tracé en fonction du temps. Le diagramme a généralement trois régions typiques[10]:
- Tout d'abord, la contrainte de cisaillement augmente en raison de la déformation en tant que réponse élastique.
- Un pic de contrainte de cisaillement est atteint en raison d'un effondrement de la microstructure du matériau. Ce point est appelé le point de rendement.
- Ensuite, une décroissance de stress due à la défaillance structurelle peut être visualisée.
Figure 11 : Détermination du point de rendement statique avec la technique de la pale (la ligne rouge représente le point de rendement)
Quelle est la différence entre la contrainte de rendement statique et dynamique ? Si la contrainte de rendement est analysée à partir d'échantillons où la structure n'est pas perturbée, on l'appelle « contrainte de rendement statique ». En revanche, si le point de rendement est analysé à partir d'échantillons qui ont été pré-cisélés avant la mesure, on l'appelle "contrainte de rendement dynamique".
Méthodes de calcul du point de rendement supplémentaires
De nombreuses fonctions de modèle supplémentaires que celles décrites dans le chapitre 3.2 sont disponibles pour déterminer le point de rendement avec une mesure de courbe d'écoulement, par exemple Casson/Steiner[11] ou Windhab[12]. Dans l'utilisation pratique, cela dépend souvent du domaine d'application lequel calcul du point de rendement conduit à de meilleurs résultats. De plus, le point de rendement d'un matériau peut également être calculé en utilisant d'autres méthodes de mesure rhéologique que celles décrites, par exemple :
- Courbes d'écoulement contrôlées par le taux de cisaillement logarithmique réalisées avec des viscosimètres/rhéomètres rotatifs
- Courbes d'écoulement contrôlées par le taux de cisaillement logarithmique réalisées avec des viscosimètres/rhéomètres rotatifs
- Les balayages d'amplitude effectués avec des rhéomètres oscillatoires à coussin d'air ; cette méthode est la plus avancée et précise disponible aujourd'hui[3].
Conclusion
On peut résumer que pour les viscosimètres/rhéomètres rotatifs qui fonctionnent selon le principe de Searle, le système de mesure tourne à une certaine vitesse, le couple correspondant est mesuré (ou vice versa), et la viscosité est calculée. De plus, une courbe d'écoulement peut être mesurée pour analyser le comportement d'écoulement de l'échantillon. Ceci est fait en augmentant le taux de cisaillement étape par étape et en déterminant la contrainte de cisaillement respective pour chaque taux de cisaillement. Un contrôle rapide du point de rendement à des fins de contrôle qualité avec un viscosimètre d'entrée de gamme peut être effectué en utilisant la technique de la pale. En ajustant le point de rendement d'un échantillon comme le ketchup ou le gel douche, la force qui est appliquée au tube lors de sa pression et donc la force nécessaire pour que l'échantillon commence à s'écouler peut être simulée.
