Notions de base de la rhéologie
La rhéologie sert à décrire et à évaluer la déformation et le comportement d'écoulement des matières. Les fluides s'écoulent à des vitesses différentes et les solides peuvent être déformés dans une certaine mesure. Huile, miel, shampooing, crème pour les mains, dentifrice, gelée sucrée, matériaux plastiques, bois et métaux – selon leur comportement physique, ils peuvent être classés dans un ordre : D'un côté les liquides, de l'autre côté les solides, et entre les deux des substances hautement visqueuses et semi-solides. Sur cette page, les principes fondamentaux – les bases de la rhéologie – sont présentés et expliqués. Il est dédié à donner une introduction à la rhéologie, fournit des informations sur les géométries de mesure et les tests rotationnels ainsi qu'oscillatoires, et contient également des définitions des termes les plus importants, tels que la contrainte de cisaillement, le taux de cisaillement ou la déformation de cisaillement. Vous trouverez également tout ce qu'il faut savoir sur les courbes d'écoulement et de viscosité ainsi que des exemples de calculs et de types de tests.
Informations liées à la rhéologie et à la rhéométrie

Académie internationale de rhéologie
L'Académie internationale de rhéologie d'Anton Paar vous donne l'opportunité d'élargir vos connaissances et d'améliorer vos compétences dans le domaine de la rhéologie.

Les rhéomètres
Solutions du leader de la connaissance en rhéométrie

Maîtriser l’écoulement
Tout l’univers de la viscosimétrie et de la rhéométrie

Rhéologie Appliquée – Avec Joe Flow sur la route de la rhéologie
Votre ressource complète en rhéologie appliquée
Rheology: Industries
Pour en savoir plus
Articles de rhéologie et glossaire
- Notions de base de la rhéologie
- Test 3iTT
- Balayages d'amplitude
- Fréquence angulaire
- Système de mesure à bille
- Analyse mécanique dynamique
- Évaluation du comportement d'écoulement dépendant du temps
- Exemples de courbe d'écoulement et de courbe de viscosité
- Exemples de calcul des gradients de cisaillement
- Détermination de la courbe et du seuil d’écoulement avec une viscosimétrie rotative
- Balayages en fréquence
- Température de transition vitreuse
- Loi de Hooke
- Comment mesurer la viscosité
- Structures internes d'échantillons et de comportement de fluidification par cisaillement
- Diagramme connexion-connexion
- Plage LVE
- Méthodes et appareils pour contrôler la température
- Loi de Newton
- Rhéologie des poudres
- Déstructuration et restructuration
- Résistance de la structure
- Comportement dépendant de la température (oscillation)
- Comportement dépendant de la température avec la réticulation ou la formation de gel
- Comportement dépendant de la température sans modifications chimiques
- Propriétés d'écoulement en fonction de la température
- Comportement dépendant du temps (oscillation)
- Comportement dépendant du temps avec la réticulation ou la formation de gel
- Tests de torsion
- Tribologie
- Seuil d'écoulement, évaluation à l’aide de la courbe d'écoulement
- Viscosité de cisaillement zéro
Puisque la rhéologie et la viscométrie sont étroitement liées, pourquoi ne pas également jeter un œil à notre page dédiée à tout ce qui concerne la viscosité et la viscométrie.
Les rhéomètres
Anton Paar propose une large gamme de rhéomètres pour répondre à différentes applications et exigences industrielles.
- Système d'analyse mécanique dynamique : MCR 702 MultiDrive
- Rhéomètre : MCR 702 MultiDrive
- Rhéomètre : MCR 102, 302, 502
- Rhéomètre : MCR 72 et MCR 92
- Rhéomètre rotatif : RheolabQC
- SmartPave : Rhéomètre à cisaillement dynamique
Introduction à la rhéologie
Rhéologie et comportement d'écoulement
La rhéologie est une branche de la physique. Les rhéologistes décrivent le comportement de déformation et d'écoulement de toutes sortes de matériaux. Le terme provient du mot grec « rhei » signifiant « couler » (Figure 1.1 : Bouteille du 19ème siècle portant l’inscription « Tinct(ur) Rhei Vin(um) Darel ». Exposé au musée des pharmacies allemandes (Musée de la pharmacie), Heidelberg. Le terme "rhei" indique que le contenu de la bouteille est liquide. La rhéométrie est la technologie de mesure utilisée pour déterminer les propriétés rhéologiques.
Quelle est la viscosité ?
Tous les liquides sont composés de molécules ; les dispersions contiennent également des particules significativement plus grandes. Lorsque mises en mouvement, les molécules et les particules sont forcées de glisser les unes sur les autres. Ils développent une résistance à l'écoulement causée par la friction interne. Des composants plus grands présents dans un fluide sont la raison des valeurs de viscosité plus élevées.Pourquoi différentes substances ont-elles des viscosités différentes ?
Les molécules dans les fluides se présentent sous différentes tailles : les molécules de solvant environ 0,5 nm, les polymères environ 50 nm (diamètre de la balle enroulée au repos), et les particules minérales environ 5 µm = 5000 nm. Un nanomètre (1 nm) équivaut à 10-9 m ; un micromètre (1 µm) est égal à 10-6 m. Cela signifie que le rapport de taille entre les molécules et les particules est compris entre 1:100 et 1:10.000 (Figure 1.2). Le rapport de 1:1000 peut être illustré par la figure suivante : Les molécules sont des poissons, chacune mesurant 10 cm (0,1 m) de long, tandis que les particules sont des navires d'une longueur de 100 m (Figure 1.3).Viscomètres rotatifs, rhéomètres oscillatoires et géométries de mesure
Les rhéomètres modernes peuvent être utilisés pour des tests de cisaillement et des tests de torsion. Ils fonctionnent avec une rotation continue et une oscillation rotative (Figure 2.1). Des systèmes de mesure spécifiques peuvent être utilisés pour réaliser des essais de traction uniaxiaux soit dans une direction de mouvement, soit comme essais oscillatoires. Avec un viscosimètre, seules les valeurs de viscosité d'un échantillon peuvent être déterminées. Cela peut être fait en effectuant des tests de rotation, principalement contrôlés par la vitesse, ou en utilisant d'autres méthodes de test. Les résultats sont présentés sous forme de courbes d'écoulement ou courbes de viscosité. Trouvez de nombreuses méthodes et approches pour mesurer la viscosité dans l' article Wiki associé. Les rhéomètres sont capables de déterminer de nombreux autres paramètres rhéologiques.


Les méthodes simples pour mesurer la viscosité incluent les systèmes de mesure relatifs dits. Les résultats obtenus dépendent toujours de l'appareil utilisé et ne peuvent pas être comparés entre eux (par exemple gobelets de débit [a,b,c] ou viscosimètres à bille tombante/roulante[d,e]). Les valeurs absolues, par exemple la viscosité, ne peuvent être déterminées qu'avec des systèmes de mesure absolus. Contrairement aux valeurs relatives, les valeurs absolues ne sont pas corrélées à la taille du système de mesure. Ils ont un écart de cisaillement relativement étroit tel que défini par des normes spécifiques pour les systèmes de mesure tels que ISO 3219[f] et DIN 53019[g]. Ces normes décrivent les géométries de mesure suivantes (Figure 2.2 et 2.3) : cône-plate, cylindres concentriques et plate-plate.
Tests rotationnels et viscosité
Tests de rotation
Des tests de rotation (Figure 3.1) avec un rhéomètre peuvent être effectués dans l'un des deux modes de fonctionnement, qui diffèrent par leurs paramètres prédéfinis (Tableaux 2 et 3). La première façon est de présenter la vitesse via la vitesse de rotation ou le taux de cisaillement (taux de cisaillement contrôlé, CSR ou CR). Cela simule des processus qui dépendent de la vitesse d’écoulement ou du débit volumétrique, comme l’application de revêtements avec une brosse, ou de peintures par pulvérisation ou flux à travers un tube (Figure 3.2). La deuxième façon est de présélectionner la force motrice via le couple ou la contrainte de cisaillement (contrainte de cisaillement contrôlée, CSS ou CS). Ces tests simulent des applications dépendantes de la force, telles que la force requise pour commencer à pomper un matériau au repos, pour expulser des matériaux d'étanchéité d'une cartouche, ou de la pâte d'un tube. La conversion du couple en contrainte de cisaillement et de la vitesse de rotation en taux de cisaillement, et vice versa, est possible via des facteurs de conversion.


| Rotation avec vitesse de cisaillement contrôlée (CSR) | Paramètres de test prédéfinis |
Résultat Données brutes du rhéomètre |
Vitesse de rotation n (en min 1) |
Couple M (en Nm) Paramètres rhéologiques, calculés |
Vitesse de cisaillement $ point gamma$ (en s 1) | Contrainte de cisaillement τ (en Pa) |
|---|
| Rotation avec contrainte de cisaillement contrôlée (CSS) | Paramètres de test prédéfinis |
Résultat Données brutes du rhéomètre |
Couple M (en Nm) |
Vitesse de rotation n (en min⁻¹) Paramètres rhéologiques, calculés |
Contrainte de cisaillement τ (en Pa) | Taux de cisaillement $ dot gamma$ (in s⁻¹) |
|---|
Pour calculer la viscosité, le type de mode d'opération est sans importance car les paramètres contrainte de cisaillement et taux de cisaillement sont tous deux disponibles, soit en tant que valeur prédéfinie, soit en tant que résultat du test. Profils prédéfinis CSR et CSS pour les courbes de flux (Figure 3.3) :
- Vitesse de rotation prédéfinie ou rampe de taux de cisaillement, généralement croissante ou décroissante par étapes
- Rampe de couple ou de contrainte de cisaillement préréglée, généralement croissante ou décroissante par étapes
Pour des taux de cisaillement supérieurs à 1 s-1, un réglage typique recommandé pour les deux modes est une durée d'au moins une à deux secondes, qui doit être maintenue pour chaque point de mesure car l'échantillon a besoin d'un certain temps pour s'adapter à chaque étape de cisaillement.
Définition des termes : contrainte de cisaillement, taux de cisaillement, loi de viscosité, viscosité cinématique
Le modèle à deux plaques est utilisé pour définir les paramètres rhéologiques nécessaires à une description scientifique du comportement d'écoulement (Figures 4.1 et 4.2). Un cisaillement est appliqué à un échantillon coincé entre les deux plaques. La plaque inférieure fixe est montée sur un support très rigide, et la plaque supérieure peut être déplacée parallèlement à la plaque inférieure. Avant de calculer la viscosité, il faut d’abord définir la contrainte de cisaillement et le taux de cisaillement.
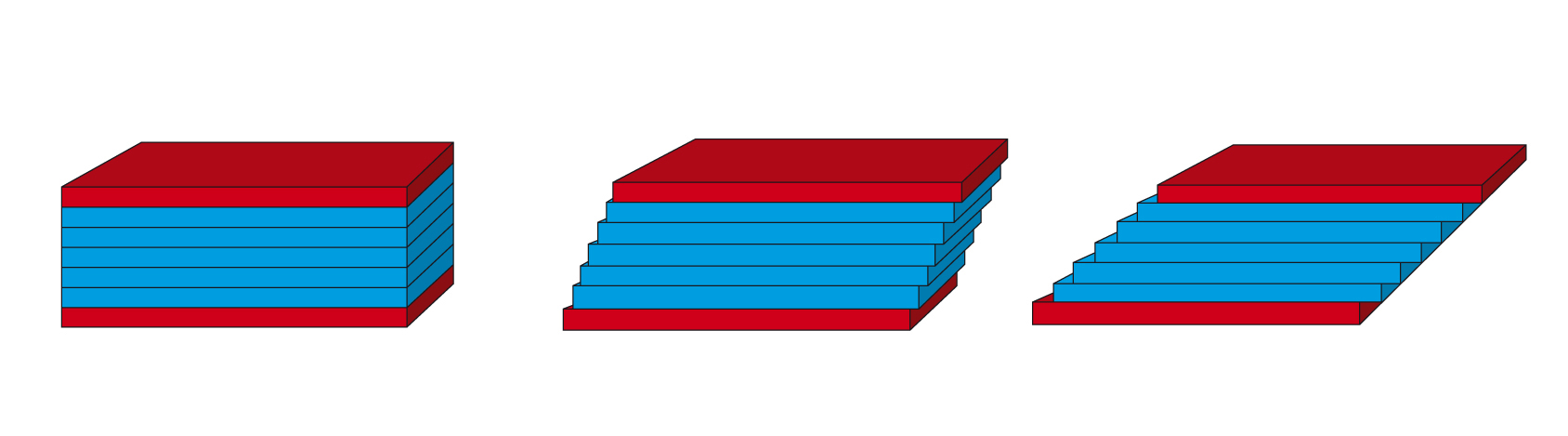
Contrainte de cisaillement
Définition: $\tau$ = F / A avec contrainte de cisaillement $\tau$ (prononcé: tau), force de cisaillement F (en N, newton) et surface de cisaillement A (en m2), voir Figure 4.3. L’unité pour la contrainte de cisaillement est 1 N/m2 = 1 Pa (pascal). Un rhéomètre enregistre la force de cisaillement via le couple à chaque point de mesure.
Gradient de cisaillement
Définition : $\dot \gamma$ = v / h avec le taux de cisaillement $\dot \gamma$ (prononcé : gamma point), vitesse v (en m/s) et espace de cisaillement h (en m), voir la Figure 4.4. L'unité de taux de cisaillement est 1/s = 1 s-1, également appelée seconde réciproque. Un rhéomètre enregistre la vitesse en tant que vitesse de rotation à chaque point de mesure. La taille de la zone de cisaillement est également connue pour le système de mesure utilisé. Trouvez des exemples pour le calcul des taux de cisaillement ici.
Viscosité ou viscosité de cisaillement / loi de la viscosité
Définition: $\eta = {\tau\over{\dot{\gamma}}}$ avec la viscosité η (prononcé: eta), contrainte de cisaillement $\tau$ (en Pa) et taux de cisaillement $\dot{\gamma}$ (en s-1), voir la Figure 4.5 (certaines valeurs de viscosité sont affichées dans le Tableau 1). Figure 4.5 : La loi de viscosité : La viscosité $ eta$ est définie comme la contrainte de cisaillement $ tau$ divisée par le taux de cisaillement $ dot{ gamma}$ (à gauche). La loi de la viscosité, ici représentée comme suit : la contrainte de cisaillement $\tau$ est le taux de cisaillement $\dot{\gamma}$ multiplié par la viscosité $\eta$ (à droite).
| Matériau fluide |
Valeurs de viscosité Gaz/air |
0,01 mPas à 0,02 mPas / 0,018 mPas Eau à 20 °C #br# (à 0 °C/ 40 °C/ 60 °C/ 80 °C/ 100 °C) |
1,0 mPas#br#(1,8 mPas/ 0,65 mPas/ 0,47 mPas/ 0,35 mPas/ 0,28 mPas) Lait, crème de café |
2 mPas à 10 mPas Huile d'olive |
Environ 100 mPas Huiles moteur#br#(par exemple SAE 10W-30, à +23 °C/ +50 °C/ +100 °C) |
50 mPas à 1000 mPas#br#(175 mPas/ 52 mPas/ 20 mPas) Fusions de polymères#br#(à T = +150 °C à +300 °C et à des taux de cisaillement compris entre 10 et 1000 s-1) |
10 mPas à 10.000 Pas Fusions de polymères#br#(viscosité à cisaillement nul, ce qui signifie des taux de cisaillement inférieurs à 1 s-1) |
1 kPas à 1 MPas Bitume à T = +80 °C/ +60 °C/ +40 °C/ +20 °C/ 0 °C |
200 Pas / 1 kPas / 20 kPas / 0,5 MPas / 1 MPas |
|---|
Les trois paramètres, à savoir la contrainte de cisaillement, le taux de cisaillement et la viscosité, ne peuvent être mesurés avec précision que s'il y a – comme condition préalable – des conditions d'écoulement laminaire et qu'il y a donc un écoulement uniforme (Figures 4.6 et 4.1). Cela signifie que l'écoulement turbulent avec formation de vortex ne doit pas se produire.
Viscosité cinématique
Un autre type de viscosité est la viscosité cinématique $\nu$ (prononcé : nu). Définition: $\nu$ = $\eta$ / $\rho$ avec la viscosité de cisaillement η (en Pas) et la densité ρ (en kg/m3). L'unité de viscosité cinématique est m2/s = 106 mm2/s. Pour les calculs, veuillez noter : Les unités de densité sont kg/m3 et g/cm3, où 1000 kg/m3 = 1 g/cm3. L'unité de viscosité de cisaillement est 1 Pas = 1000 mPas (secondes de pascal, milli-secondes de pascal). D'autres unités incluent 1 kPas = 1.000 Pas (kilo-Pas), 1 MPas = 1.000.000 Pas (méga-Pas). Une unité précédemment utilisée était 1 cP = 1 mPas (centipoise, mieux prononcé en français), mais cP n'est pas une unité SI et ne devrait plus être utilisée. La viscosité cinématique est toujours déterminée si la force gravitationnelle ou le poids de l'échantillon est la force motrice. Ceci s'applique, par exemple, aux tests avec des gobelets de débit, des viscosimètres à billes tombantes et des viscosimètres capillaires. Une unité précédemment utilisée pour la viscosité cinématique était 1 cSt = mm2/s (centistokes), mais cSt n'est pas une unité SI et ne devrait plus être utilisée. Le système SI est le système international d'unités (français : système international d’unités)[2].
Comportement d'écoulement, courbe d'écoulement et courbe de viscosité
Les valeurs de viscosité ne sont pas des valeurs constantes car elles sont affectées par de nombreuses conditions. Le sujet de ce chapitre est le comportement d'écoulement sous cisaillement à température constante. Le comportement d'écoulement peut être présenté dans deux types de diagrammes (Figure 5.1) :
- Courbes d’écoulement avec contrainte de cisaillement $ tau$ et taux de cisaillement $ point gamma$, généralement avec ce dernier tracé sur l’axe des x
- Courbes de viscosité avec viscosité η et taux de cisaillement $ dot gamma$ (ou contrainte de cisaillement $ tau$), généralement avec ce dernier tracé sur l’axe des x. En appliquant la loi de la viscosité, chaque point de mesure est calculé comme suit : $\eta$ = $\tau$ / $\dot \gamma$
Un comportement d'écoulement idéalement visqueux (ou : comportement d'écoulement newtonien) signifie que la viscosité mesurée est indépendante du taux de cisaillement (Figure 5.2, ligne 1).Les matériaux typiques de ce groupe incluent l’eau, l’huile minérale, l’huile de silicone, l’huile de salade, les solvants tels que l’acétone, ainsi que les normes de viscosité (par exemple, les huiles d’étalonnage).
Le comportement de cisaillement-diluant (ou : comportement d'écoulement pseudoplastique) se caractérise par une viscosité décroissante avec l'augmentation des taux de cisaillement (Figure 5.2, ligne 2). Les matériaux typiques qui montrent ce comportement sont les revêtements, les colles, les shampoings, les solutions polymères et les fondants polymères. Puisque la viscosité dépend de la contrainte de cisaillement, elle doit toujours être donnée avec la condition de cisaillement. Exemple : η1(${\dot \gamma}_1$) = 0.5 Pas (at 10 s-1) and η2(${\dot \gamma}_2$) = 0.1 Pas (at 100 s-1). Le comportement de fluidification par cisaillement est lié aux structures internes des échantillons. Le comportement de fluage dilatant (ou : comportement de flux dilatant) signifie une viscosité croissante avec des taux de cisaillement croissants (Figure 5.2, ligne 3). Les matériaux qui affichent généralement un tel comportement incluent des dispersions fortement remplies, telles que des suspensions céramiques (bétunes de coulée), des dispersions d'amidon, des pâtes plastisol qui manquent d'une quantité suffisante de plastifiant, des masses de remplissage dentaire (composites dentaires) ainsi que des matériaux composites spéciaux pour vêtements de protection. Pour évaluer le comportement dans la plage de faible taux de cisaillement, il est bénéfique d'utiliser un graphique log-log pour les diagrammes des courbes d'écoulement et des courbes de viscosité. L'avantage des diagrammes sur une échelle logarithmique est qu'une très large gamme de valeurs (plusieurs ordres de grandeur) peut être illustrée clairement dans un diagramme. Souvent, les plus grands changements de viscosité ont simplement lieu dans la plage des faibles taux de cisaillement, qui est inférieure à $ dot gamma$ = 1 s-1. Avec une présentation sur une échelle linéaire, cependant, cette gamme ne peut être représentée que dans une mesure limitée.
Approches pour mesurer le comportement visqueux
Le point de rendement est la valeur de contrainte de cisaillement la plus basse au-dessus de laquelle un matériau se comportera comme un fluide, et en dessous de laquelle le matériau agira comme une matière solide – parfois très douce – (selon prEN ISO 3219-1). Le point de rendement ou contrainte de rendement est la force minimale qui doit être dépassée pour détruire la structure d'un échantillon au repos, et ainsi le faire couler. La superstructure d'un échantillon peut être imaginée comme étant un réseau stable, tridimensionnel, cohérent, physico-chimique de forces interagissant entre les composants individuels de l'échantillon ; par exemple, entre les particules d'un additif de rhéologie dans une dispersion (Figure 6.1). Cliquez ici pour plus de détails et de procédures sur l'évaluation du point de rendement. Pour évaluer le comportement d'écoulement dépendant du temps, le cisaillement est maintenu constant. Pour les programmes de test avec plusieurs intervalles, cela s'applique à chaque intervalle individuel. Pour étudier le comportement dépendant du temps, il est recommandé d’effectuer un test par étapes, dans ce cas comme un test de rotation avec trois intervalles. Cette mesure est généralement réalisée sous la forme d’un test de taux de cisaillement contrôlé dépendant du temps :
- Intervalle (1) Très faible cisaillement pour simuler le comportement au repos à un taux de cisaillement faible prédéfini,
- Intervalle (2) Cisaillement fort pour simuler la défaillance structurelle de l'échantillon pendant le processus de revêtement à un taux de cisaillement élevé prédéfini, par exemple lors de l'application de peinture avec un pinceau ou par pulvérisation
- Intervalle (3) Très faible cisaillement pour simuler la régénération structurelle au repos après l’application en utilisant le même taux de cisaillement faible prédéfini que dans le premier intervalle
Voir un exemple d'application du comportement d'un revêtement de pinceau avant, pendant et après l'application (Figure 6.2).

Les méthodes d'évaluation de la régénération structurelle dépendante du temps (selon la spécification DIN 91143-2) peuvent être trouvées ici. En revanche, d'autres matériaux ne montrent aucune régénération structurelle, mais formation de gel ou durcissement sous des conditions de cisaillement constant. Pour évaluer le comportement d'écoulement dépendant du temps, le cisaillement est maintenu constant. De plus, un profil de température dépendant du temps est prédéfini. En conséquence, la fonction de la viscosité dépendant de la température est généralement évaluée. Le gradient de température dans la chambre de test entourant l'échantillon devrait être le plus petit possible. Il y a différentes méthodes et appareils disponibles pour contrôler la température. Les tests typiques dans ce domaine sont utilisés pour étudier le comportement dépendant de la température sans modifications chimiques, par exemple le comportement de ramollissement ou de fusion des échantillons lorsqu’ils sont chauffés ; ou la solidification, la cristallisation ou la gélification à froid lorsqu’ils sont refroidis (Figure 6.3). D'autres tests courants examinent le comportement dépendant de la température lors de la formation de gel ou du durcissement chimique.
Tests d'oscillation et viscoélasticité
Comportement viscoélastique
De nombreux matériaux affichent un mélange de comportement visqueux et élastique lorsqu'ils sont cisaillés (Figure 7.1). Comportement viscoélastique La section suivante traite des effets typiques causés par le comportement viscoélastique, en accordant une attention particulière à la portion élastique :

Souvent, la portion élastique du comportement viscoélastique est comparativement plus prononcée dans les conditions suivantes :
- Des mouvements plus rapides, ce qui signifie un taux de déformation ou un taux de cisaillement plus élevé, ou une fréquence d'oscillation plus élevée
- Températures plus basses : Dans les deux cas, les réseaux moléculaires seront moins flexibles et plus rigides. Plus le mouvement est lent et/ou plus la température est élevée, plus le comportement des molécules sera flexible et mobile. Il n'est donc souvent pas suffisant de déterminer la viscosité seule (avec un viscosimètre) car, dans de nombreux processus, des effets élastiques prononcés peuvent se produire. Ce mélange de comportement d'écoulement visqueux et de comportement de déformation élastique est connu sous le nom de comportement viscoélastique.
Définition des termes : déformation de cisaillement ou contrainte de cisaillement, module de cisaillement, loi de l'élasticité
Le modèle à deux plaques est utilisé pour la définition des paramètres rhéologiques nécessaires à une description scientifique du comportement en déformation (Figure 8.1). Un échantillon est découpé tout en étant coincé entre deux plaques, la plaque supérieure se déplaçant et la plaque inférieure restant stationnaire.
Contrainte de cisaillement
Définition : $\tau$ = F / A avec contrainte de cisaillement $\tau$ (prononcé : tau), force de cisaillement F (en N, newton) et surface de cisaillement A (en m2), voir Figures 8.2 et 8.3. L'unité de contrainte de cisaillement est N/m2 = Pa (Pascal).
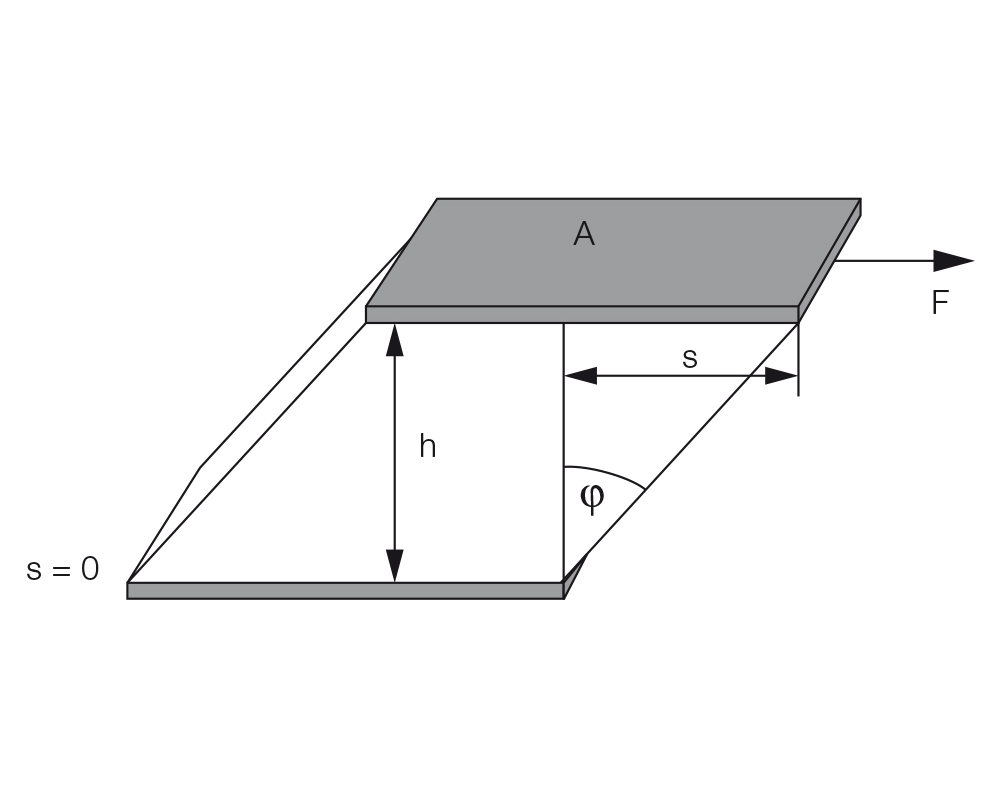
Déformation de cisaillement ou déformation de cisaillement
Définition : γ = s / h avec la déformation de cisaillement γ (prononcé : gamma), le chemin de déflexion s (en m) et l'écart de cisaillement h (en m), voir la Figure 8.4. L'unité de déformation de cisaillement est (m/m) = 1, ce qui signifie que la déformation est sans dimension. En général, la valeur est exprimée en pourcentage.
Module de cisaillement
Définition : G = τ / γ avec le module de cisaillement G, la contrainte de cisaillement τ (en Pa), et la déformation de cisaillement ou déformation de cisaillement γ (avec l'unité 1).

Approches pour mesurer le comportement visqueux
Le modèle à deux plaques peut également être utilisé pour expliquer les tests oscillatoires (Figure 9.1). Un échantillon est découpé tout en étant coincé entre deux plaques, la plaque supérieure se déplaçant et la plaque inférieure restant stationnaire. Une tige de poussée montée sur une roue motrice déplace la plaque supérieure d'avant en arrière parallèlement à la plaque inférieure, tant que la roue tourne. À vitesse de rotation constante, le modèle fonctionne à une fréquence d'oscillation également constante. Le chemin de déviation de la plaque supérieure et mobile est mesuré et évalué rhéologiquement comme contrainte ou déformation $\gamma$. Lorsque la roue de conduite se déplace, la contrainte tracée en fonction du temps donne une courbe sinusoïdale avec l'amplitude de contrainte $\gamma_A$ (Figure 9.2). Les paramètres pour les tests oscillatoires sont généralement prédéfinis sous la forme d'une courbe sinusoïdale. Pour le modèle à deux plaques, comme décrit ci-dessus, le test est un test de déformation sinusoïdale contrôlée. Une courbe sinusoïdale est déterminée par son amplitude (déviation maximale) et sa période d’oscillation. La fréquence d'oscillation est l'inverse de la période d'oscillation (Figure 9.3).
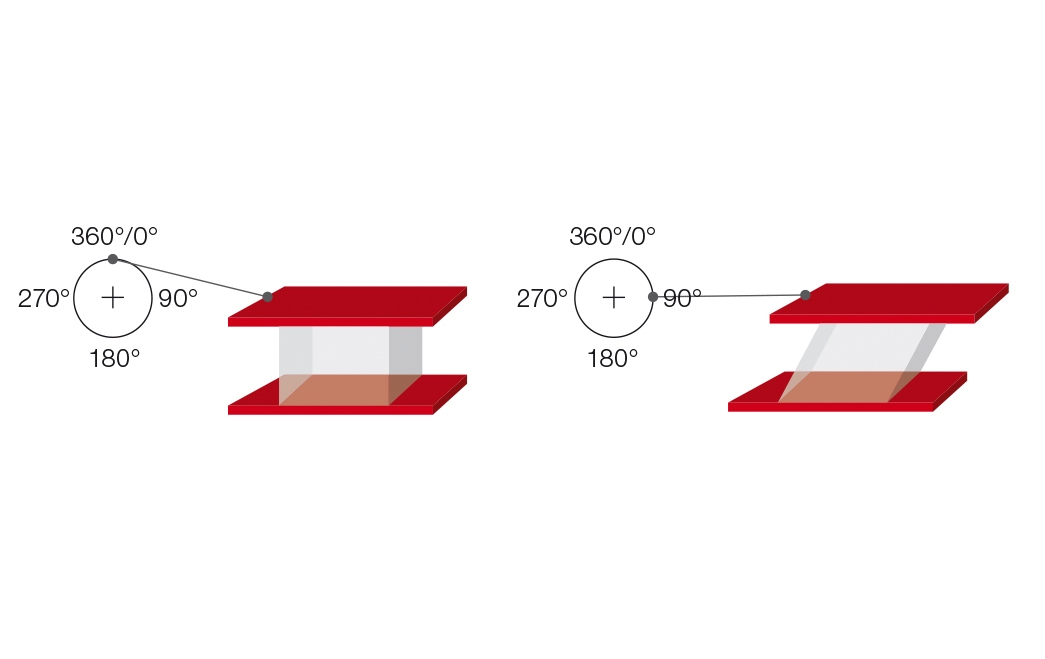
De plus, la force qui agit sur la plaque inférieure, stationnaire est mesurée. Cette force est nécessaire comme force opposée pour maintenir la plaque inférieure en position. Le signal est évalué rhéologiquement comme une contrainte de cisaillement $ tau$. Si l’échantillon n’est pas contraint par une déformation trop importante, le diagramme qui en résulte au fil du temps est une courbe sinusoïdale de la contrainte de cisaillement avec l’amplitude $ tau_A$. Les deux courbes sinusoïdales, c'est-à-dire la courbe prédéfinie ainsi que la courbe de réponse, oscillent avec la même fréquence. Cependant, si une contrainte trop importante devait être prédéfinie, la structure interne de l'échantillon serait détruite, et la courbe résultante ne serait plus sinusoïdale.
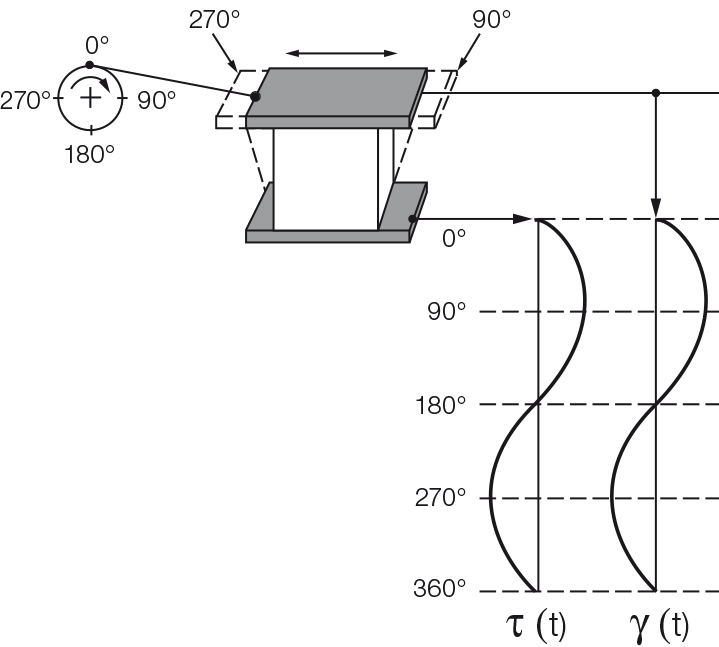

Pour un échantillon complètement rigide, tel qu'un en acier ou en pierre avec un comportement idéalement élastique, il n'y a pas de décalage temporel entre la courbe sinusoïdale prédéfinie et la réponse (Figures 9.4 et 9.5). La plupart des échantillons montrent un comportement viscoélastique. Dans ce cas, les courbes sinusoïdales du paramètre préréglé et du résultat de mesure montrent un décalage temporel pour le signal de réponse. Ce décalage est appelé le décalage de phase δ (prononcé : delta, Figures 9.6 et 9.7). C'est toujours entre 0° et 90°. Pour l'état fluide, ce qui suit est vrai : Le décalage de phase est compris entre 45° et 90°, donc 90° ≥ δ > 45°. Dans ce cas, le matériau au repos est fluide. Ce qui suit s'applique au décalage de phase : δ = 0° pour un comportement de déformation idéalement élastique et δ = 90° pour un comportement d'écoulement idéalement visqueux (Figure 9.8). Tous les types de comportement viscoélastique se produisent entre ces deux extrêmes.
Pour l'état solide, semblable à un gel, δ est compris entre 0° et 45° : c'est-à-dire, 45° > δ ≥ 0°. Dans ce cas, le matériau au repos est solide, comme des pâtes, des gels ou d'autres matières solides et rigides. Les exemples sont des crèmes pour les mains, de la gelée sucrée, des puddings laitiers et du caoutchouc pour pneus.
Module de cisaillement complexe G*
Définition de la loi de l'élasticité pour les tests de cisaillement oscillatoire : G* = τA / γA avec le module de cisaillement complexe G* (G étoile, en Pa), l'amplitude de contrainte de cisaillement τA (en Pa) et l'amplitude de déformation γA (sans dimension, ou exprimée en %). G* décrit l'ensemble du comportement viscoélastique d'un échantillon et est appelé le module de cisaillement complexe G*.
Module de stockage G' et module de perte G''
Le décalage de phase δ, qui est le temps de retard entre l'oscillation sinusoïdale prédéfinie et le résultat, est déterminé pour chaque point de mesure. Cet angle, toujours entre 0° et 90°, est maintenant placé en dessous du vecteur G* (Figure 9.9). L'axe des x s'étend de l'autre extrémité de l'angle vers la droite et l'axe des y est tracé vers le haut perpendiculairement à l'axe des x. La partie de la valeur G* qui s'étend le long de l'axe des x est la portion élastique du comportement viscoélastique présentée sous la forme de G' tandis que la partie du vecteur G* qui est projetée sur l'axe des y est la portion visqueuse G''. Cela signifie que le diagramme vectoriel complet est une présentation de G* et δ, ainsi que de G' et G'' (Figure 9.10).
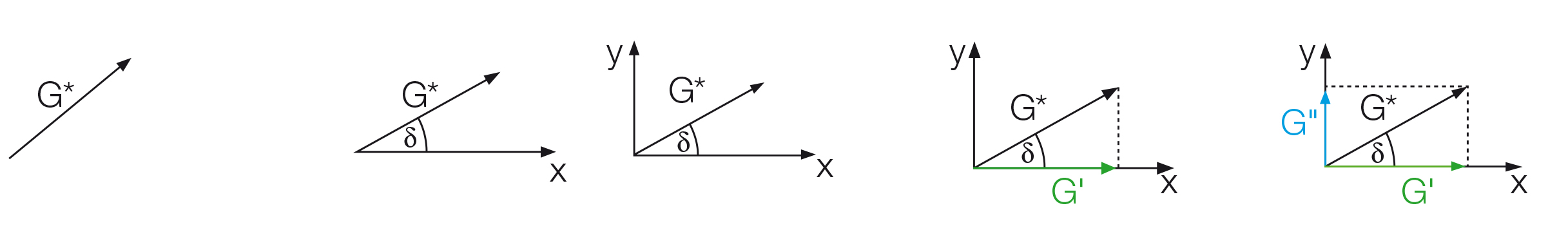

Le module de stockage G' (G prime, en Pa) représente la portion élastique du comportement viscoélastique, qui décrit quasi le comportement à l'état solide de l'échantillon. Le module de perte G'' (G double prime, en Pa) caractérise la portion visqueuse du comportement viscoélastique, qui peut être considéré comme le comportement à l'état liquide de l'échantillon. Le comportement visqueux provient de la friction interne entre les composants dans un fluide en écoulement, donc entre les molécules et les particules. Cette friction s'accompagne toujours du développement de la chaleur de frottement dans l'échantillon, et par conséquent, de la transformation de l'énergie de déformation en énergie thermique. Cette partie de l'énergie est absorbée par l'échantillon ; elle est utilisée par des processus de friction interne et n'est plus disponible pour le comportement ultérieur du matériau de l'échantillon. Cette perte d'énergie est également appelée dissipation d'énergie. En revanche, la portion élastique de l'énergie est stockée dans le matériau déformé ; c'est-à-dire en étendant et en étirant les superstructures internes sans surcharger les interactions et sans trop étirer ou détruire le matériau. Lorsque le matériau est ensuite libéré, cette énergie stockée inutilisée agit comme une force motrice pour reformer la structure dans sa forme originale. Le module de stockage G' représente l'énergie de déformation stockée et le module de perte G'' caractérise l'énergie de déformation perdue (dissipée) par le frottement interne lors de l'écoulement. Les solides viscoélastiques avec G' > G'' ont un module de stockage plus élevé que le module de perte. Ceci est dû aux liens à l'intérieur du matériau, par exemple les liaisons chimiques ou les interactions physico-chimiques (Figure 9.11). D’autre part, les liquides viscoélastiques avec G'' > G' ont un module de perte plus élevé que le module de stockage. La raison en est que, dans la plupart de ces matériaux, il n'y a pas de liaisons aussi fortes entre les molécules individuelles (Figure 9.12).
Facteur de perte ou facteur d'amortissement : tan δ = G''/ G'
(delta tangente), unité : sans dimension ou 1. Ce facteur décrit le rapport des deux portions du comportement viscoélastique. Ce qui suit s'applique (voir aussi le diagramme vectoriel à la Figure 9.10) :
- Pour un comportement idéalement élastique δ = 0°. Il n'y a pas de portion visqueuse. Donc, G'' = 0 et avec cela tan δ = G''/ G' = 0.
- Pour un comportement idéalement visqueux δ = 90°. Il n'y a pas de portion élastique. Par conséquent, G' = 0 et donc la valeur de tan δ = G''/ G' tend vers l'infini en raison de la tentative de division par zéro.
Dans certains diagrammes, le facteur de perte tan δ est tracé en plus des courbes de G' et G'', en particulier s'il y a une transition de phase dans l'échantillon. Ceci est également appelé le point de transition sol/g gel ou simplement le point de gel. Cela signifie que le caractère de l'échantillon a changé pendant la mesure de l'état liquide ou sol à l'état solide ou gel et vice versa. En général, pour des applications pratiques, un liquide est appelé idéalement visqueux si tan δ > 100:1 = 100, tandis qu'un matériau solide est appelé idéalement élastique si tan δ < 1:100 = 0,01 Les balayages d'amplitude visent généralement à décrire le comportement de déformation des échantillons dans la plage de déformation non destructive et à déterminer la limite supérieure de cette plage (Figure 9.14). Souvent, il est également intéressant de caractériser le comportement qui se produit si cette limite supérieure est dépassée avec une déformation croissante, lorsque la structure interne devient plus molle, commence à s'écouler ou se dégrade de manière fragile. Les balayages en fréquence servent généralement à décrire le comportement dépendant du temps d'un échantillon dans la plage de déformation non-destructive. Les hautes fréquences sont utilisées pour simuler un mouvement rapide sur de courtes échelles de temps, tandis que les basses fréquences simulent un mouvement lent sur de longues échelles de temps ou au repos. Dans les balayages de fréquence (Figure 9.15), la fréquence d'oscillation est augmentée ou diminuée par étapes d'un point de mesure à l'autre tout en maintenant l'amplitude constante.
Pour évaluer le comportement viscoélastique dépendant du temps, des tests oscillatoires sont effectués avec cisaillement dans des conditions dynamiques-mécaniques constantes. Cela signifie : À la fois l'amplitude et la fréquence sont maintenues constantes pour chaque intervalle de test individuel. C'est également le cas pour l'évaluation du comportement viscoélastique dépendant de la température. C'est seulement la température qui change selon un profil prédéfini. En conséquence, les fonctions dépendantes de la température de G' et G'' sont généralement analysées.
Conclusion
Les liquides à comportement visqueux et les solides à comportement élastique représentent le début et la fin de tout comportement rhéologique possible. La rhéologie est la science qui décrit les propriétés visqueuses, viscoélastiques et élastiques de différents matériaux et comment elles peuvent être influencées par :
- forces externes (ou contrainte de cisaillement)
- degré de déformation (ou contrainte de cisaillement)
- vitesse de déformation (ou taux de cisaillement)
- durée du cisaillement (et dans le cas d'un comportement thixotrope, éventuellement aussi la durée de la période de repos qui suit)
- température (par exemple de T = -150 °C à +1600 °C).
Au-delà de cela, il existe de nombreux autres paramètres rhéologiques qui peuvent affecter le comportement rhéologique. Des instruments et équipements de mesure spéciaux sont disponibles, si nécessaire. Exemples d'autres influences sur le comportement rhéologique : pression environnementale (par exemple, surpression jusqu'à 1000 bar = 100 MPa), champ magnétique ou intensité du champ électrique, rayons UV (ultraviolets) avec intensité contrôlée. Plus d'informations peuvent être trouvées dans le manuel[3] sur lequel ce Wiki, et les sous-thèmes associés, sont basés ou d'autres manuels pour une lecture complémentaire [4, 5, 6]. Si vous êtes intéressé par un séminaire ou une formation, commandez des cours eLearning[1] ou visitez les événements et séminaires Anton Paar.

Rhéologie Appliquée – Avec Joe Flow sur la route de la rhéologie
Êtes-vous prêt pour un voyage de découverte sur la route de la rhéologie avec Joe Flow ? Cette ressource complète en rhéologie appliquée est idéale pour les débutants comme pour les utilisateurs expérimentés, et comprend des idées ainsi que des conseils pratiques pour effectuer des mesures significatives de l'expert en rhéologie Thomas G. Mezger, auteur de Le Manuel de Rhéologie.



































